Robust blind source separation |
|
The unsupervised separation of components or sources is a highly challenging task. This is particularly the case when the data are corrupted with aberrant samples or outliers, which is far from being seldom when real multispectral data are considered. So far, the state-of-the-art methods are either built on using robust data fidelity term (e.g. beta-divergence) which do not allow an accurate estimation of the sources, or robust-PCA methods combined with classical BSS algorithms, which only work when the sources lie in a low-dimensional space. |
|
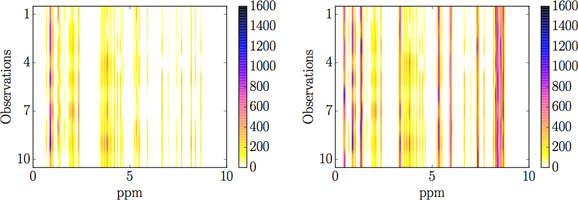
Noiseless observations (left) and corrupted observations (right) |
|
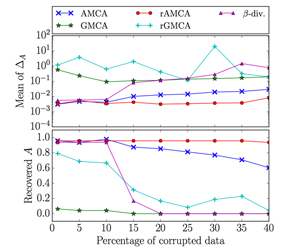
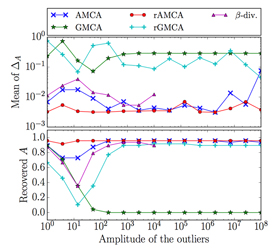
We introduce a novel robust based on the sparse modeling of both the sources and the outliers. It builds upon a recently introduced sparse blind source separation (BSS) method, the AMCA algorithm. Dubbed rAMCA, the proposed algorithms performs a joint estimation of the mixing matrix, the sources and the outliers. Furthermore, disentangling between the outliers and the sources can be efficiently tackled by exploiting the sparsity of these components as well as their different distributions in the sample domain. Indeed the sources are clustered in a subspace spanned by the columns of the mixing matrix while the outliers are assumed to be distributed in general position. These two properties are first exploited by introducing a weighting scheme to penalize the contribution of the outliers in the spirit of the AMCA algorithm. As well, we use an effective outlier estimation procedure that builds upon the difference of their distribution in the source domain. As illustrated in the figures below, the rAMCA algorithm provides the state-of-the-art performances in terms of accuracy and reliability, both in the determined and over-determined case. |
|
Separation performances as a function of amplitude (right) and percentage (left) of the corrupted entries in the determined case (the number of observations is equal to the number of sources).
|
|
Publications:
|
|
Achievements